N Traveling Salesman Problem
Therefore total time complexity is O n2 n O n O n 2 2 n Space complexity is also number of sub-problems which is O n2 n Program for Travelling Salesman Problem in C. Given a set of cities and distances between every pair of cities the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.
 Pdf A Genetic Simplified Swarm Algorithm For Optimizing N Cities Open Loop Travelling Salesman Problem Semantic Scholar
Pdf A Genetic Simplified Swarm Algorithm For Optimizing N Cities Open Loop Travelling Salesman Problem Semantic Scholar
The graph must be complete for this case so the sales.

N traveling salesman problem. The salesman has to visit each of the set of destinations starting from a particular one and returning to the same destination. TRAVELLING SALESMAN PROBLEM Travelling salesman problem adalah suatu permasalahan dalam bidang diskrit dan optimasi kombinatorial. 2 possible tours in the undirected form of the problem - n 1.
The Traveling Salesman Problem De nition. 02072021 These algorithms can be implemented to find a solution to the optimization problems of various types. If we solve recursive equation we will get total n-1 2 n-2 sub-problems which is O n2 n.
The goal is to hunt out the shortest tour that visits every town throughout a given list specifically once then returns to the beginning town 1. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. A weighted graph is a graph in which each edge is assigned a weight representing the time distance or cost of traversing that edge.
18052021 The Traveling Salesman Problem also known as the Traveling Salesperson Problem or the TSP is a well-known algorithmic problem in computer science. The traveling salesman problem is a classic problem in combinatorial optimization. Sebagai permasalahan kombinatorial persoalan ini tergolong memilingi kemungkinan jawaban yang sangat banyak.
A Hamilton circuit is a circuit that uses every vertex of a graph once. There are n 1. It is a well-known algorithmic problem in the fields of computer science and operations research.
We can use brute-force approach to evaluate every possible tour and select the best one. Each sub-problem will take O n time finding path to remaining n-1 nodes. One such problem is the Traveling Salesman Problem.
Permasalahan TSP Traveling Salesman Problem adalah permasalahan dimana seorang salesman harus mengunjungi semua kota dimana tiap kota hanya dikunjungi sekali dan dia harus mulai dari dan kembali ke kota asal. The problem says that a salesman is given a set of cities he has to find the shortest route to as to visit each city exactly once and return to the starting city. The variable no_of_locs in the code is used to define the first n.
THE TRAVELING SALESMAN PROBLEM 2 1 Statement Of The Problem The traveling salesman problem involves a salesman who must make a tour of a number of cities using the shortest path available and visit each city exactly once and only once and return to the original starting point. A cellular automata model has been developed by Dorigo and Gambardella 1997 that mimics the behavior of ants and achieves near-optimal to optimal solutions to the traveling salesman problem. 14062020 Traveling Salesman Problem.
Find the route where the cost is minimum to visit all of the cities once and return back to his starting city. The problems where there is a path between. 04112020 Travelling Salesman Problem TSP.
For three nodes A B C the tour A B C A is the same as the tour A C B A. Permasalahan ini diilhami oleh masalah seorang pedagang yang. 05122020 Thus for a traveling salesman problem for N cities location the distance matrix is of size N x N.
One sales-person is in a city he has to visit all other cities those are listed the cost of traveling from one city to another city is also provided. Since it doesnt matter which node you start at and you divide by two since eg. 02102020 Travelling salesman Problem TSP is one in every off the benchmark and previous issues in applied science and research.
Note the difference between Hamiltonian Cycle and TSP. The Travelling Salesman Problem TSP is the challenge of finding the shortest yet most efficient route for a person to take given a list of specific destinations. 12072018 Travelling Salesman Problem.
This problem is to find the shortest path that a salesman should take to traverse through a list of cities and return to the origin city. The list of cities and the distance between each pair are provided. Travelling salesman problem is the most notorious computational problem.
This cellular automata model is as good as or better than competing Operations. It consists of a salesman and a set of destinations. A complete graph K N is a graph with N vertices and an edge between every two vertices.
For n number of vertices in a graph there are n - 1. For each number of cities n the number of paths which must be explored is n. This route is called a Hamiltonian Cycle and will be explained in Chapter 2 The traveling salesman problem can be divided into two types.
With say n 15 sites there are more than 43 billion possible routes. Tujuannya adalah menentukan rute dengan jarak total atau biaya yang paling minimum. The traveling salesman problem is solved if there exists a shortest route that visits each destination once and permits the salesman to return home.
 Php Penyelesaian Traveling Salesman Problem Tsp Menggunakan Algoritma Recursive Best First Search Rbfs Elang Sakti
Php Penyelesaian Traveling Salesman Problem Tsp Menggunakan Algoritma Recursive Best First Search Rbfs Elang Sakti
 Traveling Salesman Problem Using Branch And Bound Geeksforgeeks
Traveling Salesman Problem Using Branch And Bound Geeksforgeeks
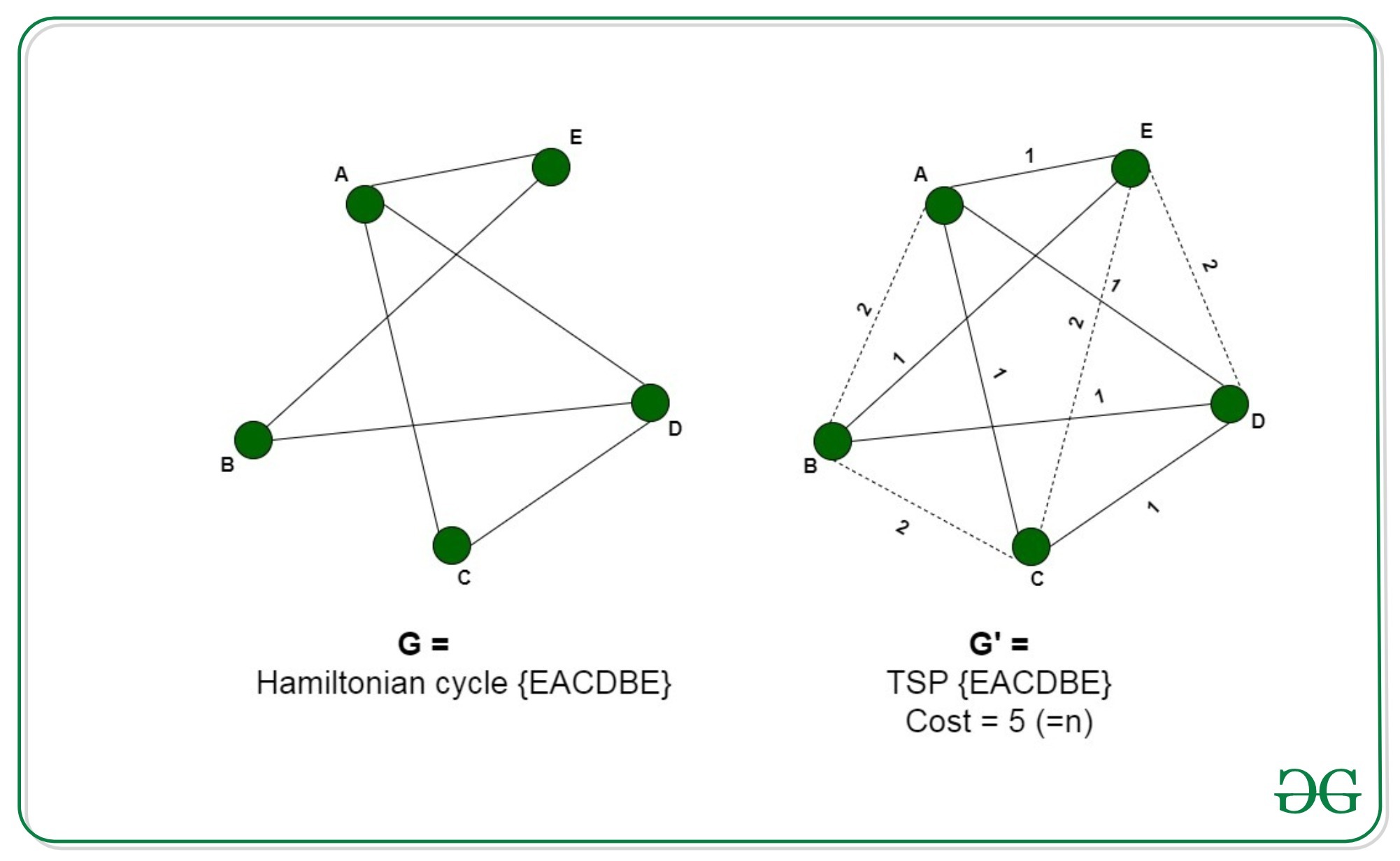 Proof That Traveling Salesman Problem Is Np Hard Geeksforgeeks
Proof That Traveling Salesman Problem Is Np Hard Geeksforgeeks
 Figure1 The Traveling Salesman Problem Tsp State Space For 4 Cities Download Scientific Diagram
Figure1 The Traveling Salesman Problem Tsp State Space For 4 Cities Download Scientific Diagram
 Chapter 10 The Traveling Salesman Problem
Chapter 10 The Traveling Salesman Problem
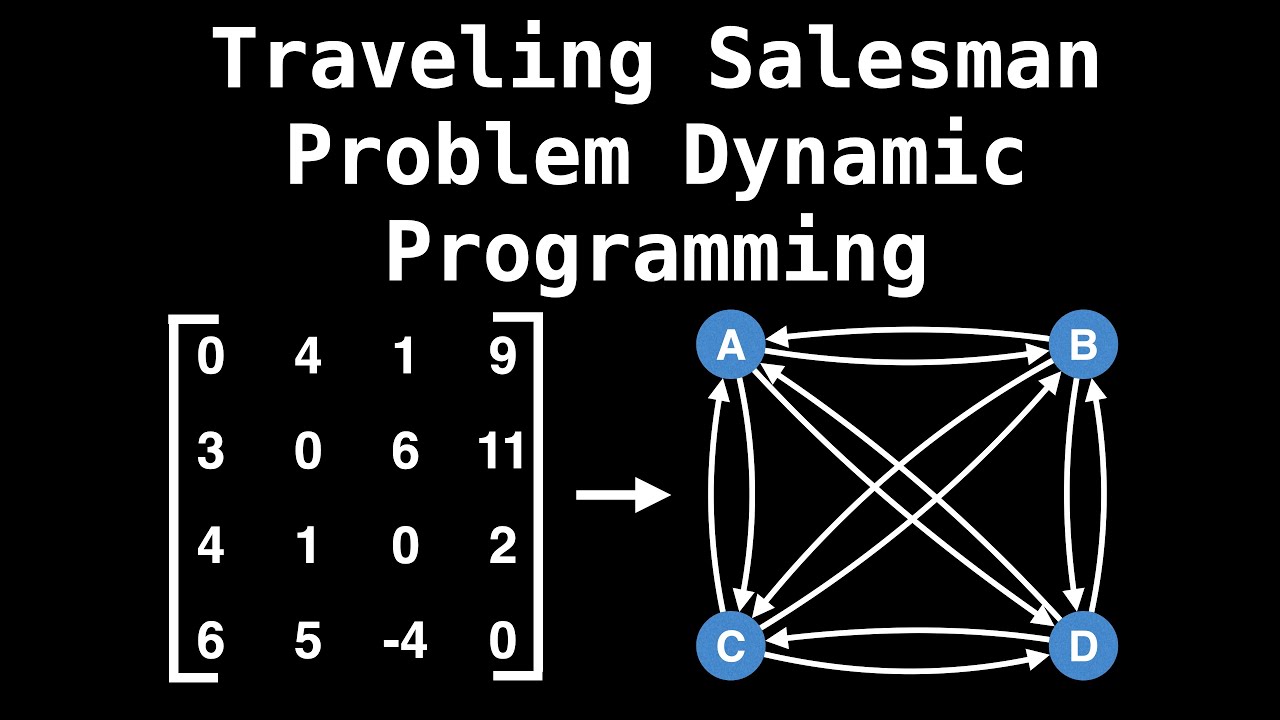 Travelling Salesman Problem Dynamic Programming Graph Theory Youtube
Travelling Salesman Problem Dynamic Programming Graph Theory Youtube
 Two Types Of Open Loop Travelling Salesman Problem A Classic Open Download Scientific Diagram
Two Types Of Open Loop Travelling Salesman Problem A Classic Open Download Scientific Diagram
 Daa Traveling Salesman Problem
Daa Traveling Salesman Problem
Posting Komentar untuk "N Traveling Salesman Problem"